Focus
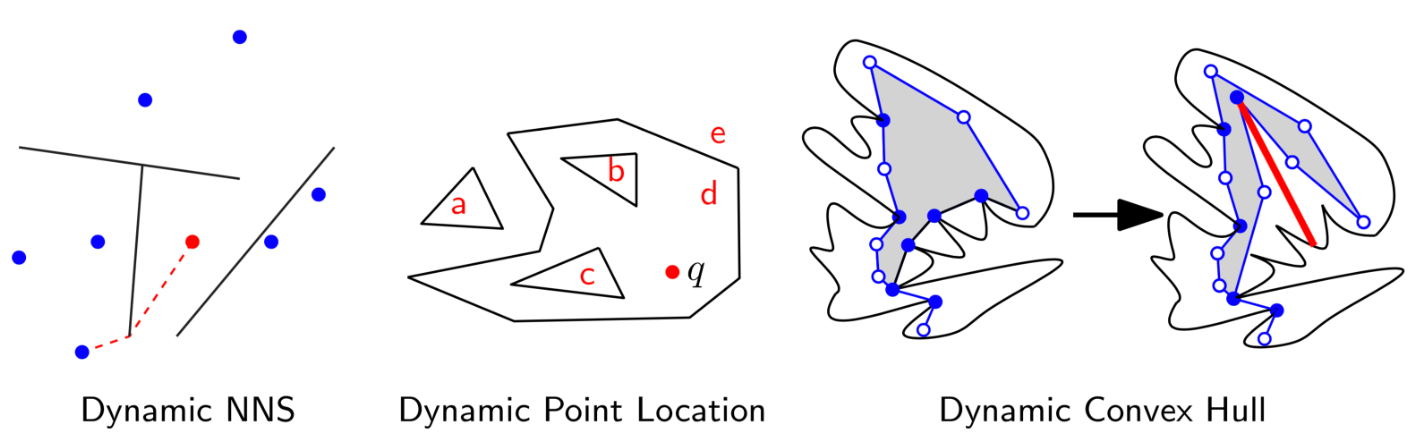
Currently, we are interested in designing algorithms and data structures that could solve various problems in dynamic environments. The problems that we are interested include nearest neighbor search, point location, Voronoi diagram, and convex hull. We seek to find ways to extend already known efficient algorithms in static environments to work in dynamic environments.
Also, we are applying algorithms in computational geometry to solve various geometric problems in the practical world, such as navigation system, teeth alignment, and semiconductor design.
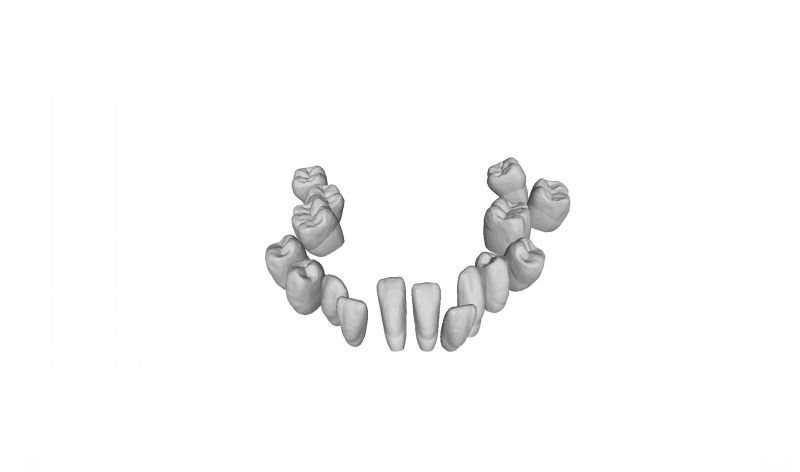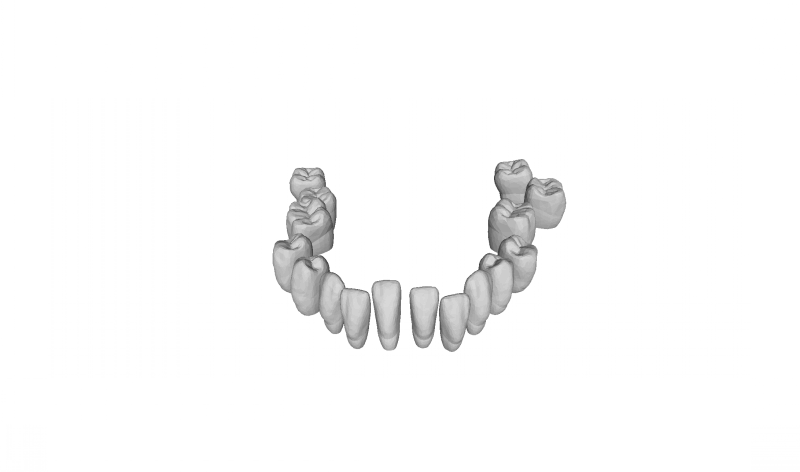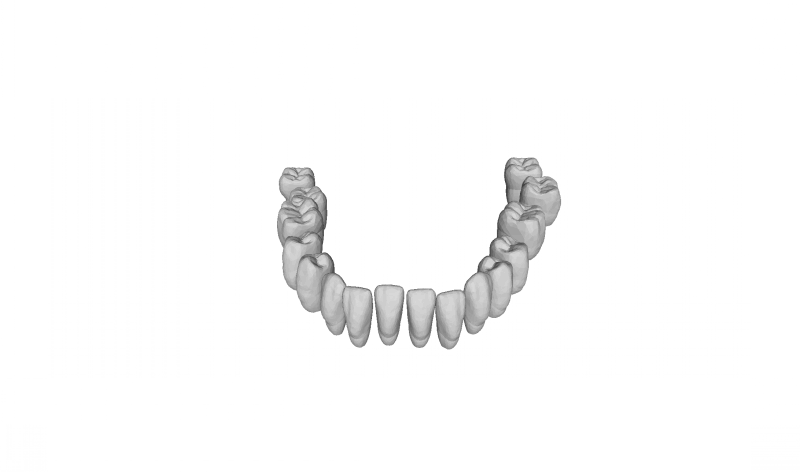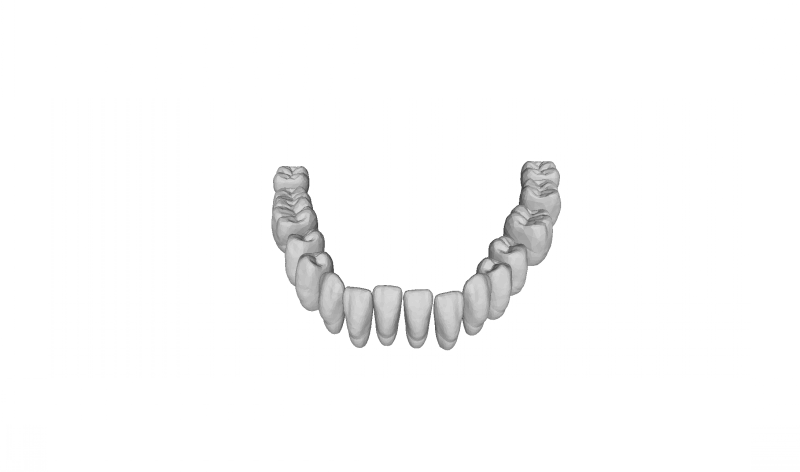
Geometric Shape Matching is an important ingredient in shape retrieval, recognition and classification, alignment and registration, and approximation and simplification. In a large database of shapes, for example, shape retrieval searches for all shapes similar to a query shape.
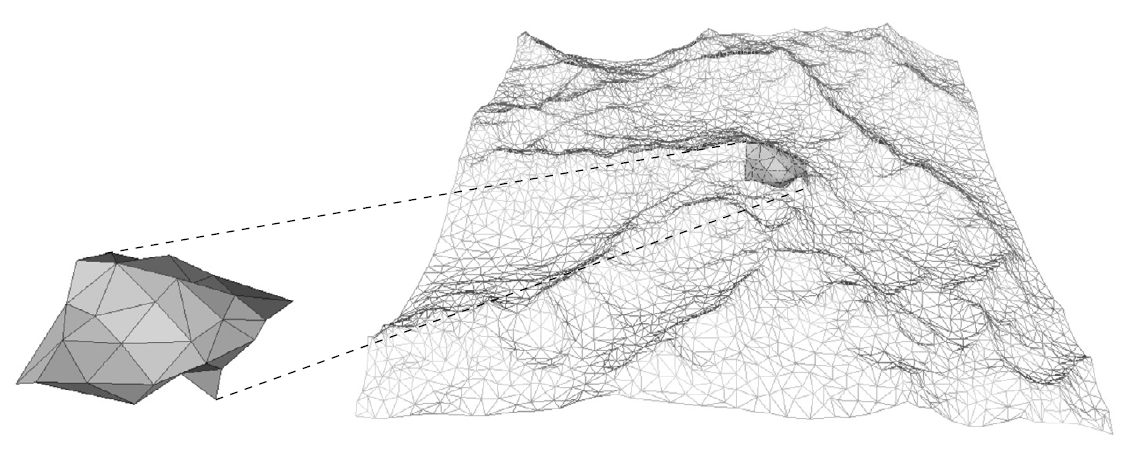
Shape Approximation: Substituting a complex geometric shape by a “simpler” one is motivated by many applications. A typical example is the problem of computing the smallest (area) enclosing disc (or annulus, square, …) of a given set of points in d-dimensional Euclidean space.
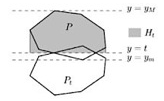
Unfortunately many of these problems turn out to be computationally difficult. Many of them areNP-hard, and for many others the best known solutions have polynomial runtimes of high degree which renders these algorithms uninteresting from a practical point of view. A possible solution is that instead of insisting on computing the exact solution for such an optimization problem, one looks for a solution that approximates the optimum reasonably well.
Skyline queries have gained much attention lately in database and data mining communities, as formulating such queries is rather intuitive compared to other types of queries, for example, ranking. However, not much has been known about Spatial Skyline Queries, skyline queries on massive spatial data. We study spatial skyline query processing problem, which enables an intelligent and efficient access to massive spatial data.
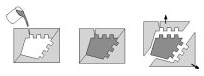
In Casting, liquid is poured into a cast that has a cavity with the shape of the object to be manufactured. The liquid then hardens, after which the cast is removed and one is left with an object whose shape is that of the cavity. The key property necessary for casting is that the cast parts can be removed from the object without destroying either the cast parts or the object. This ensures that the given object can be mass produced by re-using the same cast parts.
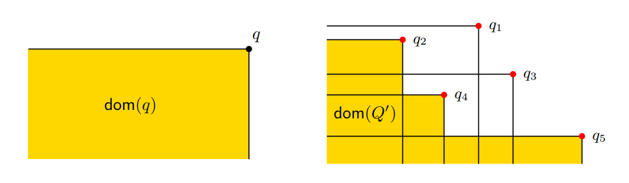
Dominance problem is one of the important problem in computational geometry. Our result maximizing dominance in the plane implies algorithms with better time bounds for related problems, including the disjoint union of cliques problem for interval graphs (equivalently, the hitting intervals problem) and the top-k representative skyline points problem in the plane.