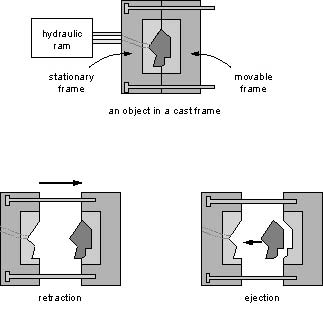
Geometric Aspects of the Casting Process


The process of casting in real world
Casting Geometric Aspects of the Casting Process
Manufacturing is the process of converting raw materials (such as iron, glass or polymer) to useful products, ranging from goods such as kettles and telephones to machinery such as railway locomotives and aircrafts. By means of computer-aided design (CAD) and computer-aided manufacturing (CAM), these manufacturing processes have been done in a form of automation, both in design phase and construction phase. Due to the geometric nature of manufacturing processes, many geometric problems has arised in it. Computational geometry arises at all levels of manufacturing, from design, modeling and simulation, to process planning, on-line verification and testing. 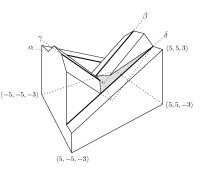In casting, liquid is poured into a cast that has a cavity with the shape of the object to be manufactured. The liquid then hardens, after which the cast is removed and one is left with an object whose shape is that of the cavity. The key property necessay for casting is that the cast parts can be removed from the object without destroying either the cast parts or the object. This ensures that the given object can be mass produced by re-using the same cast parts.
Papers published or submitted for publication
Separating an Object from its Cast We consider the case where the cast consists of two parts and address the following problems. (1) Given a cast for an object and a direction d, can the cast be partitioned into two parts such that the parts can be removed in directions d and -d, respectively, without colliding with the object or the other cast part? (2) How can one find a direction d such that the above cast partitioning can be done? We give necessary and sufficient conditions for both problems, as well as algorithms to decide them for polyhedral objects. with Mark de Berg, Prosenjit Bose, Siu-Wing Cheng, Dan Halperin, Jirí Matousek, and Otfried Schwarzkopf In Proc. 13th Annu. ACM Symposium on Computational Geometry, 221--230, 1997 and in Computer-Aided Design, 34(8):547-559, 2002
Casting with Skewed Ejection Directions We give necessary and sufficient conditions to test the feasibility of the cast part retraction and object ejection, where retraction and ejection directions need not be the same. For polyhedral objects, we show that the test can be performed in O(n^2\log^2 n) time and the cast parts can be constructed within the same time bound. The complexity of the cast parts constructed is worst-case optimal. We also give a polynomial time algorithm for finding a feasible pair of retraction and ejection directions for a given polyhedral object. with Siu-Wing Cheng, and Otfried Cheong In Proc. 9th Annu. International Symposium on Algorithms and Computation, 1998, and in Algorithmica, 44(4):325-342, 2006
Casting with Directional Uncertainty We consider directional uncertainty: given a 3-dimensional polyhedral object, is there a polyhedral cast such that its two parts can be removed in opposite directions with uncertainty \alpha without inflicting damage to the object or the cast parts? We give a necessary and sufficient condition for castability, and a randomized algorithm that verifies castability and produces two polyhedral cast parts for a polyhedral object of arbitrary genus. Its expected running time is O(n\log n). The resulting cast parts have O(n) vertices in total. We also consider the case where the removal direction is not specified in advance, and give an algorithm that finds all feasible removal directions with uncertainty \alpha in expected time O(n^2\log n/\alpha^2). with Otfried Cheong, and René van Oostrum In Proc. 13th Annu. International Symposium on Algorithms and Computation, 2002, and in Computational Geometry: Theory and Applications, 26(2):129-141, 2003
The Reflex-Free Hull We propose a hull operator, the reflex-free hull, that allows us to define a 3D analogue to bays in polygons. The reflex-free hull allows a rich set of topological types, yet for polyhedral input with $n$ edges, it remains a polyhedral set with O(n) edges. This is in contrast to other possible hull definitions that give non-planar surfaces and higher combinatorial complexity. The reflex-free hull is related to identifying cavities in computer aided design and manufacturing, but we sketch examples to indicate that computing a reflex-free hull will be a challenging problem. with Siu-Wing Cheng, Otfried Cheong, and Jack Snoeyink In Proc. 13th Canadian Conference on Computational Geometry, 2001, and in International Journal of Computational Geometry and Applications, 14(6):453-474, 2004
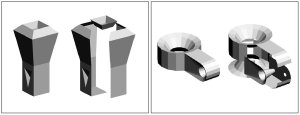
Casting an Object with a Core This paper addresses geometric problems that concern manufacturing an object using a cast with a core. In casting, molten material is poured into the cavity of the cast and allowed to solidify. The cast has two main parts to be removed in opposite parting directions. To manufacture more complicated objects, the cast may also have a core to be removed in a direction skewed to the parting directions. In this paper, given an object and the parting and core directions, we give necessary and sufficient conditions to verify whether a cast can be constructed for these directions. In the case of polyhedral objects, we develop a discrete algorithm to perform the test in $O(n^3\log n)$ time, where $n$ is the object size. If the test result is positive, a cast with complexity $O(n^3)$ can be constructed within the same time bound. We also present an example to show that a cast may have $\Theta(n^3)$ complexity in the worst case. Thus, the complexity of our cast is worst-case optimal. with Sang-Won Bae, Siu-Wing Cheng, and Kyung-Yong Chwa In Proc. 16th Annual International Symposium on Algorithms and Computation 2005. To appear in Algorithmica.
More details available [ PDF] My thesisis available [ online]